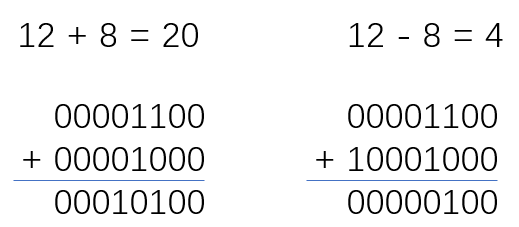计算机内可以存储各种各样的数据,例如:文本数据、图片数据、音频数据、视频数据等等。
这些数据都会以 位(bit,或比特) 的形式储存在计算机内,并且它们的组织形式通常是一组,我们一般认为 8个位为 1个字节(byte)。
计算机能处理的位数越多,那么它的速度就会越快。接下来,这篇文章会向读者介绍计算机是如何对其中的数据进行处理的。
整数
人类的计数方式通常是“逢十进一”,称为 十进制(Decimal),大概因为人有十个手指,所以十进制是最自然的计数方式,很多民族的语言文字中都有十个数字,而阿拉伯数字0~9是目前最广泛采用的。
计算机是用数字电路搭成的,数字电路中只有1和0两种状态,或者可以说计算机只有两个手指,所以对计算机来说 二进制(Binary) 是最自然的计数方式。根据“逢二进一”的原则,十进制的1、2、3、4分别对应二进制的1、10、11、100。
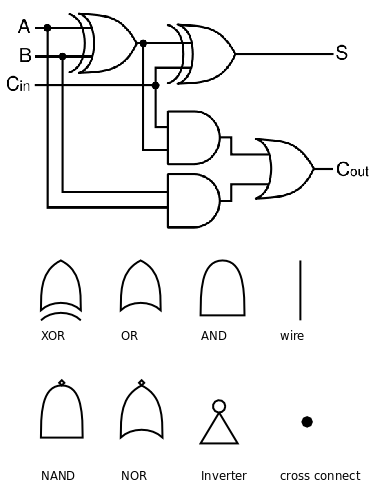
计算机采用如下的逻辑电路计算两个 bit 的加法:
Sign and Magnitude表示法
我们如果用 8个 bit 表示正数和负数,那么一个简单的想法就是把最高位规定为 符号位(Sign Bit),这样一个字节的取值范围就是 -$2^7$-1 ~ $2^7$-1。
-1 - 10000001
+1 - 00000001
- 1.两个数的低7位相加的结果超出了范围,就会产生 溢出(Overflow),这时通常把计算机中的一个标志位置1表示当前运算产生了溢出。
- 2.两个符号位不同的数,一个大一个小,用大的数减小的数,符号位是大数的符号位。
- 3.零的表示有两种,一种是符号为 0 的正零,另一种是符号为 1 的负零。
- 4.两个数做减法的时候就需要进行转换,把加数先变成负数然后再进行加法运算。
我们可以发现,如果采用Sign and Magnitude表示法,计算机做加减运算需要处理很多逻辑:比较符号位,比较绝对值,加法改减法,减法改加法,小数减大数改成大数减小数……这是非常低效率的。
Complement表示法
一种更好的方法就是用二进制补码系统来表示有符号整数,因为它可以将减法运算转换为对减数的补数运算。
补码的类型有两种:1位补码(1’s complement)和2位补码(2’s complement)。
- 一位补码:
- 也称为原码。
- 正数的一位补码与其本身相同。
- 负数的一位补码为其绝对值的二进制形式,所有数字位取反,再加一。
- 二位补码:
- 也称为反码。
- 正数的二位补码与其本身相同。
- 负数的二位补码为在原码的基础上,符号位不变,其余位取反,再加一。
补数运算:
以十进制为例,如果一个数是一位的,那么它与它的补数和总是 9,这样 2 的补数是 7;如果这个数是两位的,那么补数和就是99,那么 11 的补数是 88。
以二进制为例,通常是 $n$ 位的运算,那么数 $P$ 的补数为 $Q$ 且 $P + Q = 2^n$。例如,01100101 的补数和是 100000000,求一个数的补数是取反加 1,这样 01100101 的补数就是 10011010 + 1 = 10011011。
如果两个正数相加溢出,结果一定是负数;如果两个负数相加溢出,结果一定是正数;一正一负相加,无论结果是正是负都不可能溢出。如果溢出了,就要连接到溢出标志位去提示计算产生了溢出。
无符号二进制乘法
我们回顾一下平时使用的乘法,就是先把乘数的一部分先与被乘数相乘,记录下每个部分的乘积然后再将它们相加得到最终的结果。
但实际上,计算的做法稍微有些不同,它在每次做运算的时候就先将部分积的值加到乘数中。
布斯乘法
布斯乘法适用于,两个正数、一个正数和一个负数、两个负数相乘的情况。它与无符号数乘法很相似,我们对算法进行描述:
对于 $N$ 位乘数 $Y$ ,布斯算法检查其 2 的补码形式的最后一位和一个隐含的低位,命名为 $y[i-1]$ ,初始值为 0 。对于 $y[i], i = 0, 1, …, N - 1$,考察 $y[i]$ 和 $y[i - 1 ]$。当这两位相同时,存放积的累加器 $P$ 的值保持不变。当 $y[i] = 0$ 且 $y[i - 1] = 1$ 时,被乘数乘以 $2^i$ 加到 $P$ 中。当 $y[i]= 1$ 且 $y[i - 1] = 0$ 时,从 $P$ 中减去被乘数乘以 $2^i$ 的值。算法结束后, $P$ 中的数即为乘法结果。
同样是 10x13 的这个例子,我们用布斯乘法计算无符号的乘法:
上述式子结果高位溢出直接丢弃,结果就是:1000 0010。
如果是对于无符号位的计算,则需要先将负数用原码进行表示,然后再进行计算:
上述式子结果高位溢出直接丢弃,结果就是:00 1000 0010。
除法
除法就是通过被除数不断减去除数直到结果为零或小于除数来实现的。
减去除数的次数为 商(quotient),最后一次减法的差为 余数(remainder)。
与乘法的部分积类似,除法的话主要是对部分被除数做减法。
我们先看看无符号除法的例子,575 ÷ 25:
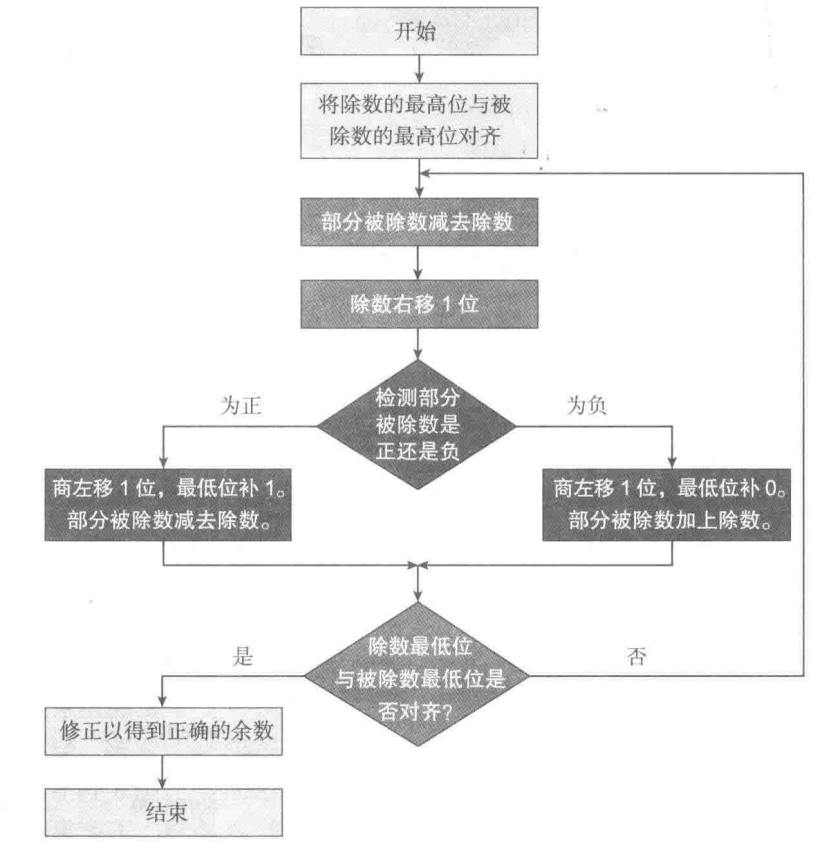
我们需要用文字描述这一个过程的实现,主要用以下这两种表述:
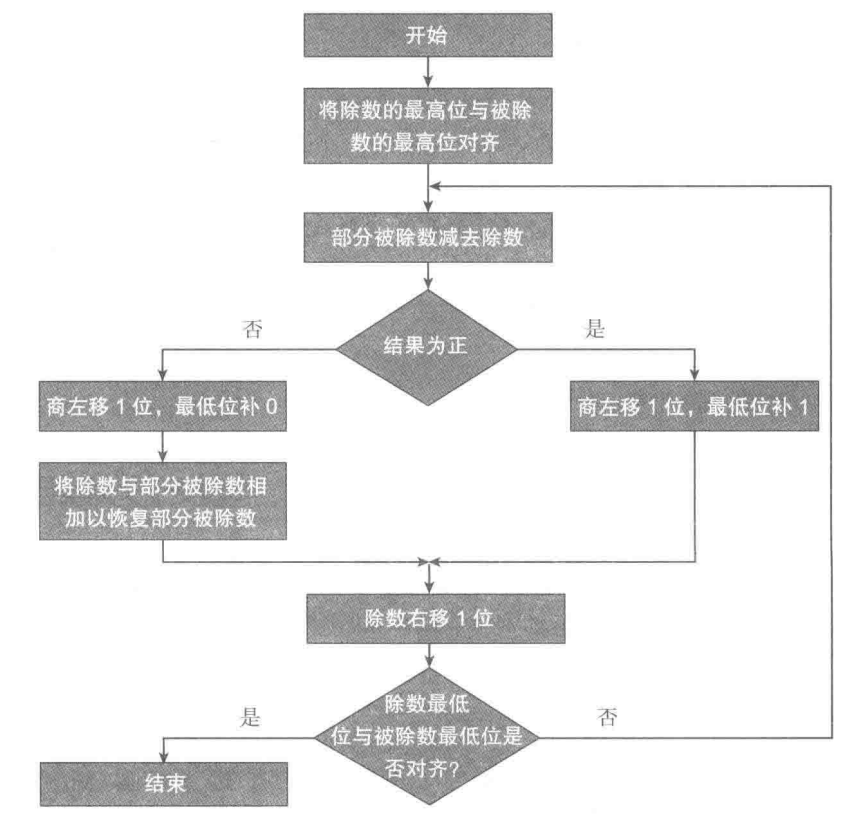
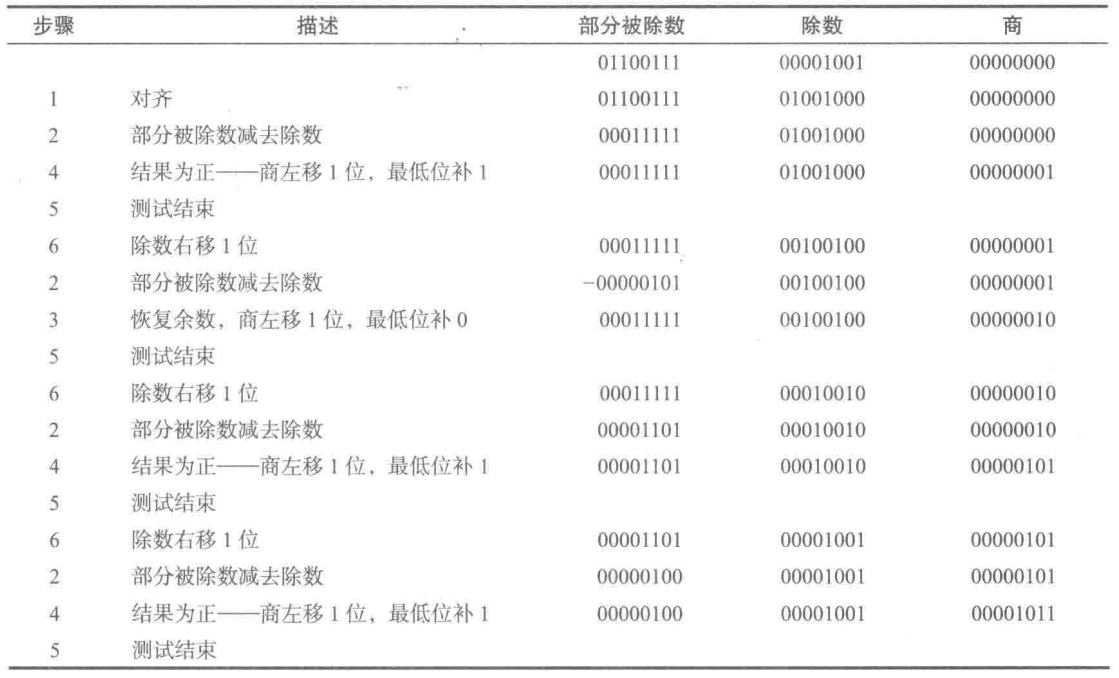
1.恢复余数除法
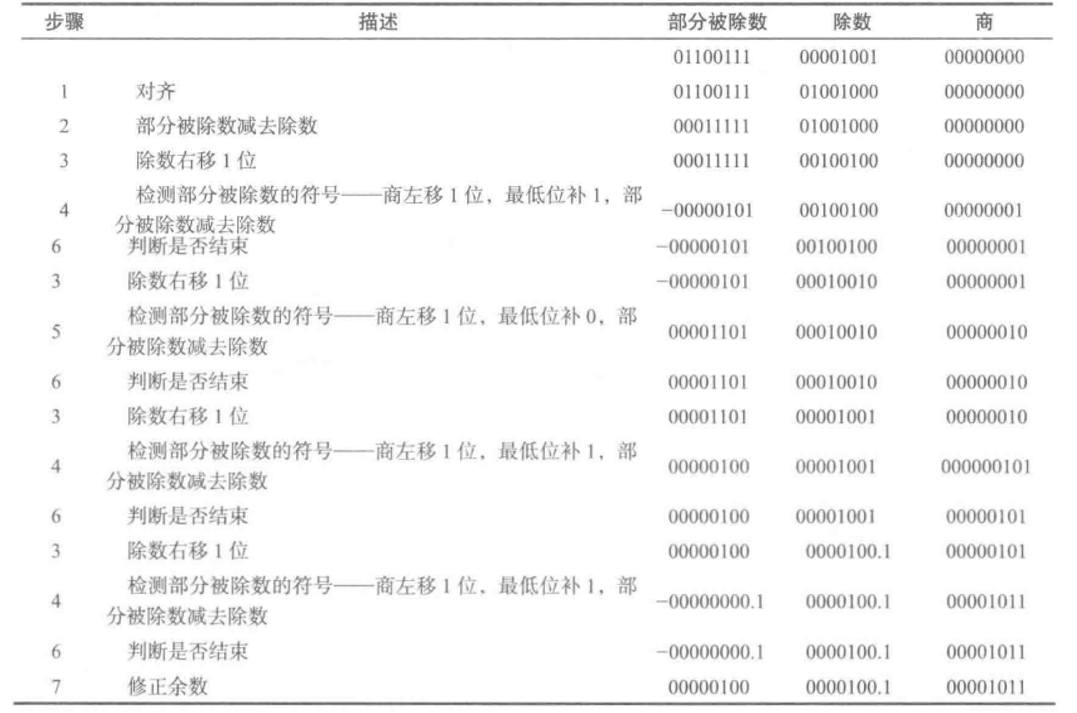
部分被除数初始化为被除数,除数对齐是通过位移实现的,书上的例子很清晰,这里就直接贴图,不做另外的解释了。
2.不恢复余数除法
浮点数
浮点数运算就是实数之间的运算,它不像整数运算,浮点数的计算结果一般是不确定的。
浮点数表示也被称作 “科学计数法”,在十进制运算中,科学计数法表示的数字被写成:尾数 x $10^{指数 }$ 的形式,例如:$1.2345 \times 10^{20}$,指数以 10 的整数倍将其扩大或缩小。
二进制浮点数则表示为:尾数 x $2^{指数 }$,例如:$1.01010111 \times 2^5$。
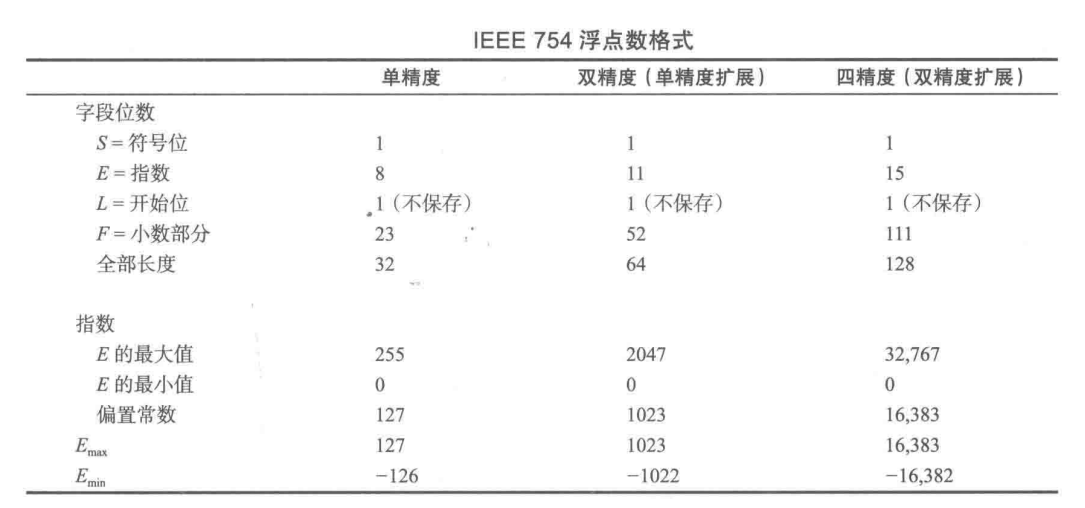
IEEE 754 浮点数标准提供了 3 种浮点数表示:32 位单精度浮点数,64 位双精度浮点数,以及 128位四精度浮点数。
IEEE(电气和电子工程师协会)
电气和电子工程师协会 (IEEE, 读做 “eye- triple-ee”) 是一个包括所有电子和计技术的专业团体。它出版刊物,举办会议,并且建立委员会来定义标准,内容涉及从电力传输到软件工程。另一个 IEEE 标准的例子是无线网络的 802. 11 标准。
IEEE 浮点表示
IEEE 浮点标准采用 $V = (-1)^s \times F \times 2^{E - 偏置常数}$ 的形式来表示一个数:
- 符号(sign)$s$ 决定这个数是负数还是正数。
- 尾数(significand)$F$ 是一个二进制小数。
- 阶码(exponent)$E$ 的作用是对浮点数加权,$E_{min}-1$ 表示浮点 0,$E_{max}+1$ 表示正或负无穷大或 非数(Not a Number, NaN)。
为什么对指数进行偏置?(以单精度浮点数为例)
因为单精度浮点数的指数部分使用 8 位来存储(范围:0~255),为了能够表示正负的指数所以我们减去一个偏移量得到:-126~+127。
十进制转换为二进制浮点数
将十进制数 $4100.125_{10} $ 转换为符合 IEEE 754 标准的 32位单精度二进制浮点数。
首先将 $4100.125$ 转换为二进制定点数,整数部分 $4100_{10} = 10000000000100_2$,小数部分 $0.125_{10}=0.001_2$,所以 $4100.125_{10} = 10000000000100.001_2$。
接下来对该二进制数进行规格化,就是将小数点左移变成 1.xxx 的形式,每左移动一次指数就加一:$1.0000000000100001 \times 2^{12}$。
- S = 0
- E = 12 + 127 = 10001011
- F = 00000000010000100000000
浮点运算
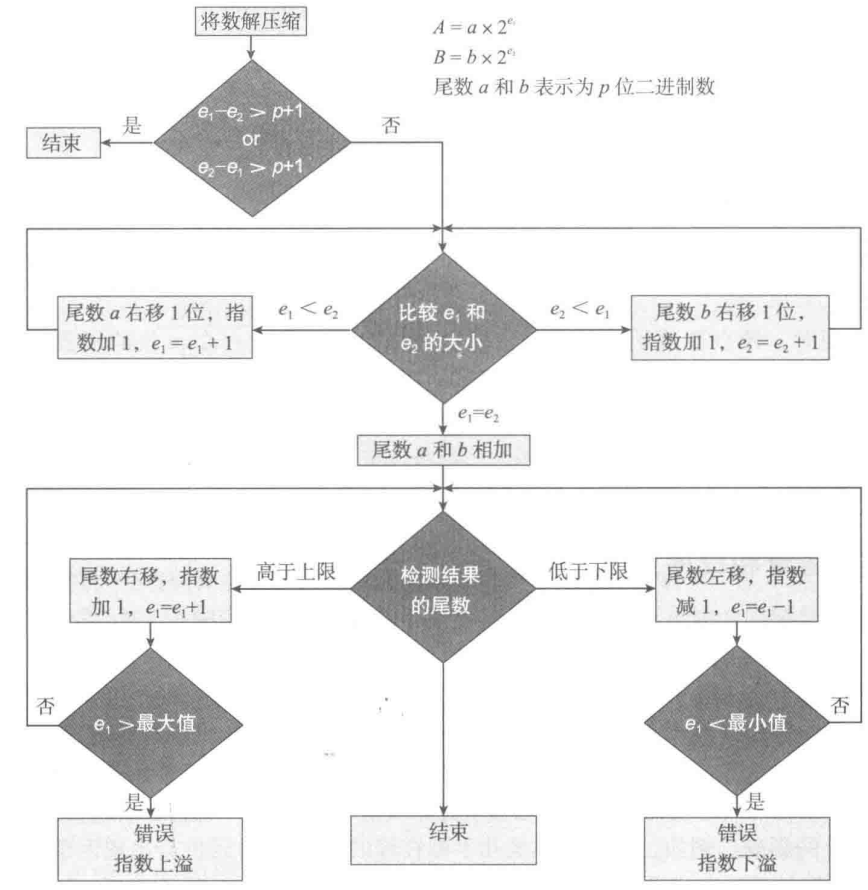
浮点数不能直接相加,我们要先对齐浮点数的小数点,然后使它们的指数大小相同,然后才对尾数进行运算,最后再对结果进行规格化。
下面给出书上的流程图,但要注意几点:
- 因为指数有时和尾数位于同一个字中,所以在加法过程开始之前要将它们分开。
- 如果两个指数的差大于 $p+1$ ,这里 $p$ 为尾数的位数,那么较小的数就无法影响大的数。
- 结果规格化的时候会检查指数,看它是是否比最小指数小或比最大指数大,分别检测指数下溢或上溢,下溢会导致结果为 0,上溢会造成结果错误。