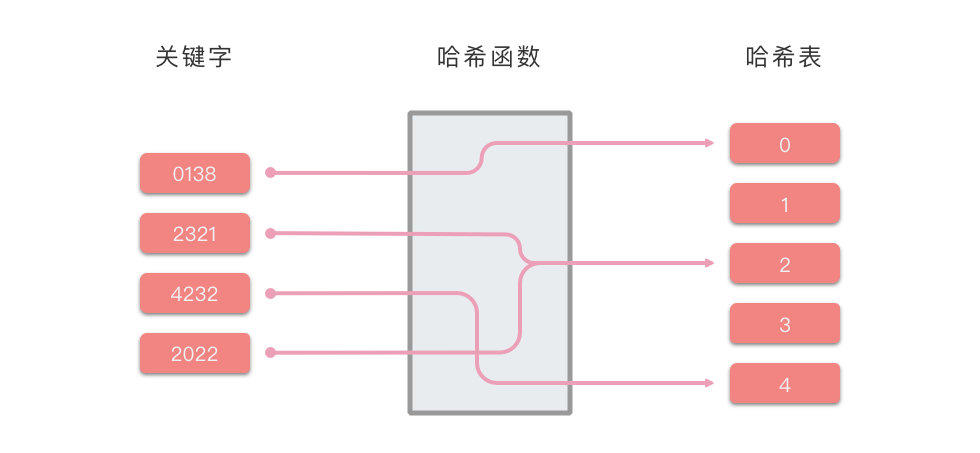
哈希表平衡二叉树红黑树

哈希表

哈希表（Hash Table） 也是散列表，通过键值对来进行数据访问的数据结构。

哈希表的作用就是我们能用比较快的速度来对数据进行检索，我们已经很熟悉的字典、映射等数据结构的底层都是用哈希表来做的实现。

哈希表是这样的，它的里面维护着一个数组，数组的大小不会很大也不会很小。同时，哈希表里面还有哈希函数（Hash Function），是用来计算哈希值的。

首先，一个键值对的数据给到哈希表，它先根据“键”计算该键的哈希值，然后再放在对应的数组位置上，这样不同的哈希值的数据就被放到不同的数组位置上了。

但是，实际情况并不可能这么完美，所以会有哈希值一样的情况，也就是哈希冲突（Hash Collision），当然我们有各种各样的方法来解决哈希冲突，后面我们来介绍。

哈希函数作为哈希表的最重要组成部分，一般是要满足以下条件：

下面是一些常用的哈希函数：

直接定址法：用”键“的线性函数来做哈希地址。
- $ Hash(key) = a\times key+b$，其中 $a$ 和 $b$ 都是常数。
除留余数法：如果数组长为 $m$ 就取一个大于 $m$ 但是接近或等于 $m$ 的质数 $p$ ，利用取模运算，将关键字转换为哈希地址。
- $Hash(key)= key \kern 5pt mod \kern 5pt p$。
平方取中法：先通过求关键字平方值的方式扩大相近数之间的差别，然后根据表长度取关键字平方值的中间几位数作为哈希地址。
- $Hash(key)=(key\times key)//100\kern 5pt mod\kern 5pt 1000$，先计算平方，然后除去后两位数，再取中间 3 位作为哈希值。

但是在实际中，我们通常会用一些标准哈希算法，例如 MD5、SHA-1、SHA-2 和 SHA-3 等。它们可以将任意长度的输入数据映射到恒定长度的哈希值。

**哈希冲突（Hash Collison）**就是不同的关键字通过哈希函数计算出了相同的结果的情况。

常见的处理方式有两种：开放地址法（Open Addressing）、链式地址法（Separate Chaining）。

（1）开放地址法（Open Addressing）：

通过探测的方式找到哈希表中的空位置，直到哈希表被全部填满为止。
它通过这样的方法来去求后继的哈希地址：$H(i) = (Hash(key) + F(i)) \kern 5pt mod \kern 5pt m $。
其中，$F(i)$ 是冲突解决方法：
- 线性探测法：$F(i) = 1,2,3,\dots,m-1$。
- 二次探测法：$F(i)=1^2,-1^2,2^2,-2^2,\dots,±n^2$。
- 伪随机数序列：$F(i)=伪随机数序列$。

（2）链式地址法（Separate Chaining）：